How To Find Standard Deviation Of Two Data Sets

Standard Deviation of a Information Set

Definition of the Standard Deviation

The standard departure is a measure of how close the data values in a data ready are from the mean. It is a quantity that is small when data is distributed close to the mean and big when data is far form the mean.
allow x₁, 10_two, 10_three ... x_N exist a set of data with a mean μ. To mensurate how far is a data value x_i from the hateful, we may employ the difference d_i given by
d_i = x_i - μ
The trouble with the higher up definition is that d_i may be negative or positive and when you add all the d_i for all information values to obtain an average, they may cancel each other. Hence nosotros square d_i average them and so the square root.
The standard deviation σ of a population having N elements is defined by

\sigma =\sqrt {\dfrac{\sum_{i=1}^{North} (x_i - \mu)^ii}{North}}

where

\mu = \dfrac{\sum_{i=i}^{N} x_i}{N}

In a statistical report, we may have large populations and therefore computing the standard departure for the whole population may be plush and time consuming hence the idea of using samples from the population to estimate the standard deviation.
The standard difference south of a data set up of a sample having Due north elements is defined by

south =\sqrt {\dfrac{\sum_{i=1}^{N} (x_i - \overline{x})^2}{N - 1}}

where

\overline{x} = \dfrac{\sum_{i=one}^{N} x_i}{Northward}

The primary deviation betwixt the two formulas is the division by North and North - 1. We use North - one in the formula of the standard deviation for samples to compensate for the fact that the number of data values in a population is much larger than the number of data values in a sample. Annotation too that for Due north very large, the two formulas would give very close values.
An online calculator to compute the standard deviation is included.

Examples on Standard Deviation

Example 1
Three data sets representing three populations are given below.
A:{ane,1,15,15} B:{1,7,9,15} C:{7,7,ix,9}
Calculate the mean and the standard departure for each information gear up. Compare the means and the standard deviation of the iii sets.
Solution to Example 1
For set A

\mu_A = \dfrac{1 + 1 + 15 + 15 + 11}{iv} = 8

\sigma_A=\sqrt {\dfrac{(ane - 8)^2 + (1 - 8)^2 + (xv - 8)^2 + (15 - 8)^2}{4}} = 7

For fix B

\mu_B = \dfrac{1 + 7 + ix + xv}{v} = eight

\sigma_B =\sqrt {\dfrac{(1 - 8)^2 + (7 - 8)^2 + (9 - viii)^2 + (xv - eight)^2}{4}} = v

For fix C

\mu_C = \dfrac{7 + 7 + 9 + 9}{4} = viii

\sigma_C =\sqrt {\dfrac{(7 - 8)^2 + (7 - 8)^2 + (ix - 8)^two + (9 - 8)^2}{iv}} = 1

The means of the three sets are equal to eight (cherry dot in graph) and the standard deviations are different. We can see on the graphs on the number lines below of the three sets. It is graphically articulate that the information values in Set C are close to the hateful and that is why this fix has the smallest standard deviation. The graphs on the number line of set A and B shows that information in Set A is more than dispersed than the data in fix B, hence the standard deviation is gear up A is larger than of set up B.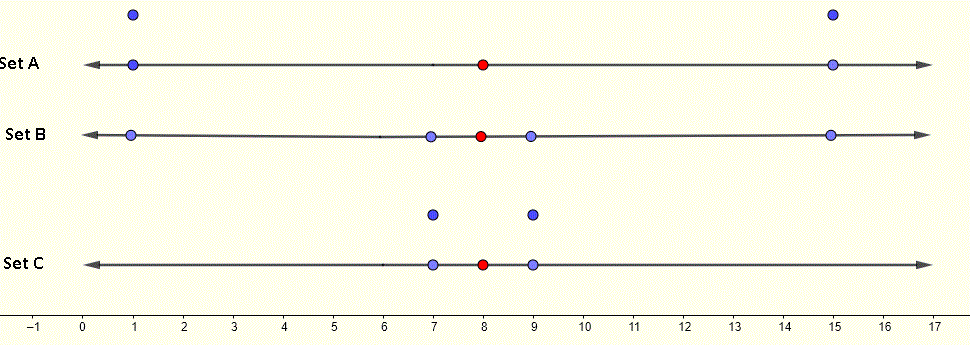 Set A, Set B ans Set C on a number line

Example 2
Two information sets representing two populations are given below.
A:{2 , 3 , v , 8 , ten} B:{3 , 4 , 6 , 9 , 11}
Calculate the mean and the standard deviation for each data set. Compare the ways and the standard divergence of the two sets.
Solution to Example two
For set A

\mu_A = \dfrac{2 + 3 + five + viii + 10}{five} = five.six

\sigma_A=\sqrt {\dfrac{(2 - 5.half dozen)^two + (3 - five.half-dozen)^2 + (five - 5.6)^two + (viii - 5.6)^2 + (10 - 5.6)^2}{5}}

=3.0

For set B

\mu_B = \dfrac{3 + iv + 6 + 9 + 11}{five} = 6.6

\sigma_B =\sqrt {\dfrac{(2 - v.6)^2 + (3 - five.half-dozen)^2 + (5 - 5.6)^2 + (8 - 5.6)^2 + (x - five.6)^2}{v}}

=iii.0

The means are different and the standard deviation are equal. This means the data values in the two sets are distributed in the same manner around the hateful. The two sets A and B are shown below on number lines. Although the ii sets are dissimilar, the distances between the data values and the mean are correspondingly equal and that explains why the two sets have equal standard deviations. Set A and Set B on a number line

Example 3
The scores in a Physics exam of students in two classes A and B have the following ways and standard deviations.
Form A: hateful = 78 and standard divergence = five
Grade A: mean = 78 and standard difference = xv
What tin nosotros conclude almost the performance of students in the two classes?
Solution to Case iii
The scores of the two classes have equal ways but the standard deviation of course B is higher than the standard deviation of course A. This means that the scores in class B are more dispersed and therefore in class B and therefore some students might have scored much lower then the mean while other students might have scored much college than the hateful. In general students in class A scored closer to the hateful.
Instance four
The hateful of a set of data values is equal to μ and its standard departure is equal to σ. If all the information values in the set are increased by the aforementioned value yard, what is the hateful and the standard deviation afterward the increase?
Solution to Case 4
If yous plot all data values on a number line and add k to these values and graph them once again on the same number line, all points on the number line would be shifted by the same altitude k and therefore the mean besides increases by k. However the standard departure will not change because it is a measure of the distance between the data values and the mean and they all shifted by the same value k.
The mean and standard deviation of the set { x_1, x_2 ,... x_N } are given by

\mu = \dfrac{\sum_{i=1}^{N} x_i}{Northward}

and

\sigma =\sqrt {\dfrac{\sum_{i=ane}^{North} (x_i - \mu)^2}{Northward}}

We at present add k to each data value x_i and compute the mean and standard deviation

\mu_k = \dfrac{\sum_{i=one}^{N} (x_i + chiliad)}{N} = \dfrac{\sum_{i=1}^{N} x_i}{N} + \dfrac{\sum_{i=1}^{North} k}{N} = \mu + k

\sigma_k =\sqrt {\dfrac{\sum_{i=1}^{North} ((x_i + thou) - \mu_A)^two}{N}} = \sqrt {\dfrac{\sum_{i=1}^{Northward} (x_i + k - (\mu + k))^ii}{N}}

Simplify the numerator to obtain

\sigma_k = \sqrt {\dfrac{\sum_{i=one}^{N} (x_i - \mu )^2}{North}}

Hence if we increase all data values in a ready by the same amount grand, the mean increases by grand but the standard deviation does non alter.