How To Find X In A Triangle With Degrees

Triangle Calculator

Please provide 3 values including at least one side to the following 6 fields, and click the "Calculate" button. When radians are selected as the angle unit, information technology can take values such equally pi/2, pi/four, etc.




Bending Unit:

A triangle is a polygon that has three vertices. A vertex is a point where two or more curves, lines, or edges meet; in the case of a triangle, the iii vertices are joined past 3 line segments called edges. A triangle is normally referred to by its vertices. Hence, a triangle with vertices a, b, and c is typically denoted as Δabc. Furthermore, triangles tend to be described based on the length of their sides, as well as their internal angles. For example, a triangle in which all three sides have equal lengths is called an equilateral triangle while a triangle in which 2 sides accept equal lengths is called isosceles. When none of the sides of a triangle have equal lengths, it is referred to equally scalene, as depicted below.

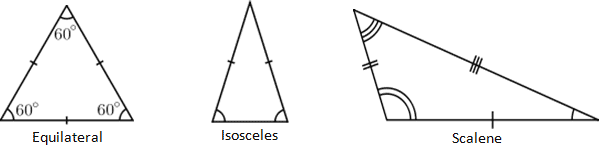
Tick marks on the edge of a triangle are a common notation that reflects the length of the side, where the same number of ticks ways equal length. Similar notation exists for the internal angles of a triangle, denoted past differing numbers of concentric arcs located at the triangle's vertices. Every bit tin be seen from the triangles higher up, the length and internal angles of a triangle are directly related, so information technology makes sense that an equilateral triangle has three equal internal angles, and three equal length sides. Note that the triangle provided in the calculator is not shown to scale; while it looks equilateral (and has angle markings that typically would be read as equal), information technology is not necessarily equilateral and is simply a representation of a triangle. When actual values are entered, the figurer output will reverberate what the shape of the input triangle should await like.

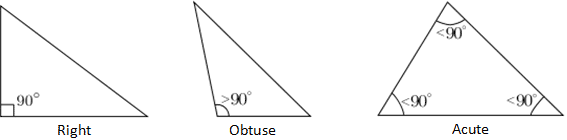
Triangles classified based on their internal angles fall into ii categories: right or oblique. A right triangle is a triangle in which 1 of the angles is 90°, and is denoted by two line segments forming a foursquare at the vertex constituting the correct angle. The longest edge of a right triangle, which is the edge reverse the correct angle, is called the hypotenuse. Any triangle that is not a right triangle is classified as an oblique triangle and can either be obtuse or acute. In an obtuse triangle, one of the angles of the triangle is greater than 90°, while in an acute triangle, all of the angles are less than 90°, as shown below.

Triangle facts, theorems, and laws

It is non possible for a triangle to accept more than ane vertex with internal angle greater than or equal to 90°, or it would no longer be a triangle.
The interior angles of a triangle always add up to 180° while the exterior angles of a triangle are equal to the sum of the 2 interior angles that are not adjacent to it. Another way to summate the outside angle of a triangle is to subtract the angle of the vertex of interest from 180°.
The sum of the lengths of whatsoever ii sides of a triangle is always larger than the length of the third side
Pythagorean theorem: The Pythagorean theorem is a theorem specific to right triangles. For any correct triangle, the foursquare of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides. It follows that whatsoever triangle in which the sides satisfy this condition is a correct triangle. In that location are also special cases of right triangles, such equally the xxx° 60° xc, 45° 45° 90°, and 3 4 5 correct triangles that facilitate calculations. Where a and b are two sides of a triangle, and c is the hypotenuse, the Pythagorean theorem can exist written as:
a² + bⁱⁱ = c^two
EX: Given a = 3, c = 5, find b:
iii² + b² = v^two
9 + b² = 25
b² = 16 => b = 4
Police force of sines: the ratio of the length of a side of a triangle to the sine of its opposite angle is constant. Using the police of sines makes information technology possible to detect unknown angles and sides of a triangle given plenty information. Where sides a, b, c, and angles A, B, C are as depicted in the higher up calculator, the law of sines can be written every bit shown beneath. Thus, if b, B and C are known, it is possible to observe c by relating b/sin(B) and c/sin(C). Note that there exist cases when a triangle meets certain weather condition, where two different triangle configurations are possible given the aforementioned prepare of data.

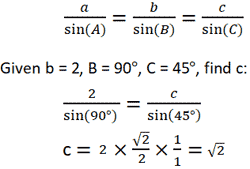
Given the lengths of all iii sides of whatever triangle, each angle tin be calculated using the following equation. Refer to the triangle above, bold that a, b, and c are known values.

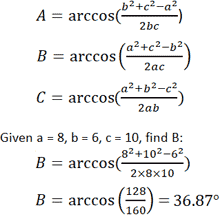
Surface area of a Triangle

At that place are multiple different equations for calculating the area of a triangle, dependent on what data is known. Likely the most commonly known equation for computing the area of a triangle involves its base, b, and height, h. The "base" refers to any side of the triangle where the pinnacle is represented by the length of the line segment fatigued from the vertex opposite the base, to a bespeak on the base of operations that forms a perpendicular.

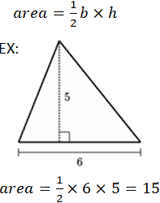
Given the length of 2 sides and the angle between them, the following formula can exist used to determine the area of the triangle. Notation that the variables used are in reference to the triangle shown in the computer above. Given a = nine, b = 7, and C = 30°:

Another method for computing the area of a triangle uses Heron's formula. Different the previous equations, Heron's formula does not require an arbitrary selection of a side as a base, or a vertex as an origin. However, it does require that the lengths of the iii sides are known. Again, in reference to the triangle provided in the reckoner, if a = three, b = 4, and c = 5:

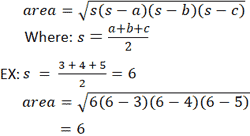
Median, inradius, and circumradius

Median

The median of a triangle is divers every bit the length of a line segment that extends from a vertex of the triangle to the midpoint of the opposing side. A triangle can take iii medians, all of which will intersect at the centroid (the arithmetics mean position of all the points in the triangle) of the triangle. Refer to the effigy provided beneath for clarification.

The medians of the triangle are represented by the line segments thou_a, m_b, and grand_c. The length of each median can be calculated as follows:

Where a, b, and c represent the length of the side of the triangle as shown in the figure above.

As an example, given that a=2, b=3, and c=four, the median one thousand_a can exist calculated as follows:

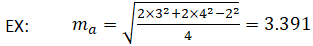
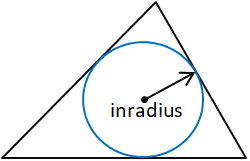
Inradius

The inradius is the radius of the largest circle that will fit inside the given polygon, in this case, a triangle. The inradius is perpendicular to each side of the polygon. In a triangle, the inradius can be adamant past constructing 2 angle bisectors to determine the incenter of the triangle. The inradius is the perpendicular altitude between the incenter and one of the sides of the triangle. Any side of the triangle tin exist used as long equally the perpendicular distance between the side and the incenter is determined, since the incenter, by definition, is equidistant from each side of the triangle.

For the purposes of this calculator, the inradius is calculated using the surface area (Area) and semiperimeter (southward) of the triangle along with the following formulas:

where a, b, and c are the sides of the triangle

Circumradius

The circumradius is defined as the radius of a circumvolve that passes through all the vertices of a polygon, in this case, a triangle. The centre of this circle, where all the perpendicular bisectors of each side of the triangle meet, is the circumcenter of the triangle, and is the point from which the circumradius is measured. The circumcenter of the triangle does not necessarily have to be inside the triangle. It is worth noting that all triangles have a circumcircle (circle that passes through each vertex), and therefore a circumradius.